Note: This was originally posted on 26 October 2018, but it had mysteriously disappeared from my blog in early 2020, and a database restore from backup did not bring it back, so I recreated it, mostly from memory. Update: The posts have mysteriously rematerialized, but I’m keeping this post up in case the old post disappears again.
A recurring question of philosophy concerns whether or not things that have highly complex order/structure can result from random events or accidents and, more specifically, whether or not complex information can result from randomness/accidents. That last question was examined as early as the mid 1st-century B.C. by Cicero, a Roman contemporary of Julius Caesar, in Book 2 of his “Tusculan Disputations.” Cicero’s great rhetorical skills not withstanding, he lacked any formal mathematical method to effectively prove his case. Today we have such a method in the mathematics of probability, thanks largely to the heavy lifting of 17th-Century mathematicians like Blaise Pascal, Abraham de Moivre, and Christiaan Huygens. By the mid-19th century A.D., one answer to this question about the origin of complex information is what has come to be known as the Infinite Monkey Theorem, which may seem merely whimsical until you realize that the monkey here is just a symbol for randomness. The Infinite Monkey Theorem is actually a legitimate probability proof that shows how complex information will occur at random, given an infinite number of random data event generators–such as monkeys randomly tapping away at keyboards–or just one such random data event generator operating for an infinite amount of time. The event spaces are infinite, either in scope or duration, and therefore encompass all possibilities with respect to complex information.
The problem with the Infinite Monkey Theorem is that it’s not a particularly meaningful answer to this question about the origin of complex information. Today, we know the Universe to be finite: It had a definite beginning, a finite amount of time has transpired since the Big Bang, and we can infer that the Universe therefore has finite boundaries encompassing a finite amount of matter, energy, and space-time. If we want a meaningful answer to this question about the origin of complex information, we need to therefore re-evaluate scenarios like the Infinite Monkey Theorem from a finite perspective. Scholars and scientists have been doing just that for at least the past 50 years, and one such scholar was an electrical engineering professor at the University of Colorado. Richard A Roberts passed away in 1990, but one of his text books was published posthumously (An Introduction to Applied Probability. Addison-Wesley, 1992, ISBN-10: 020105552X), and in the chapter covering repeated independent trials, Roberts re-examined the Infinite Monkey Theorem with finite dimensions.
Example 3.5.2
Suppose a billion monkeys type on word processors at a rate of 10 symbols per second. Assume that the word processors produce 27 symbols, namely 26 letters of the English alphabet and a space. These monkeys type for 10 billion years. What is the probability that they can type the first sentence of Lincoln’s “Gettysburg Address”?
Fourscore and seven years ago our fathers brought forth on this continent a new nation conceived in liberty and dedicated to the proposition that all men are created equal.
Solution: If we counted correctly, there are 168 symbols in this sentence. Let N be the number of symbols typed per monkey in 1010 years. A sample space of possible letter sequences typed by each monkey is
S = X * X * … * X (N times)
where X is the set of 27 symbols. Now define s as a particular sequence that is m symbols long:
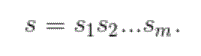
Let Ak be the event that s appears at the kth index in a sequence of length N:
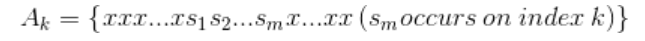
In other words, Ak is the event that a particular sequence, s, which is m symbols long, appears in one monkey’s sequence and ends on index k. The event of interest is A, given by
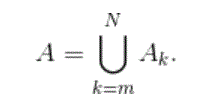
In our case, m = 168 and N is the number of symbols typed by one monkey in 1010 years. Thus by Boole’s Inequality,
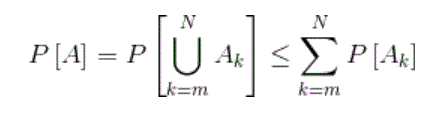
Now the probability of the event Ak is the number of outcomes of event Ak divided by the total number of outcomes. The total number of outcomes is 27N. The number of outcomes that produce event Ak is 27N-m. The exponent is N-m because there are m positions specified in Ak. The remaining N-m are arbitrary. Thus
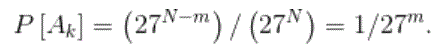
And so
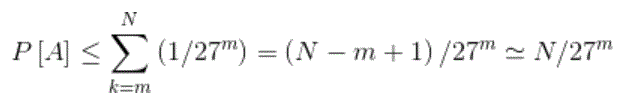
since N >> m. Thus P[A] is bounded above by N/27m, where N is the number of trials produced by a single monkey. That is the probability bound for P[A] for one monkey. For 109 monkeys, we can think of forming one long sequence by concatenating 109 sequences so that N becomes the number of trials produced by 109 monkeys. Thus P[A] is bounded above by
P[A] ≤ (109)(107 sec/year)(10 symbols/sec)(1010 years) ≅ 1027/10240 ≤ 10-213.
The probability of producing a specified sequence of English text 168 symbols long is bounded above by 10-213. No reasonable model for the source of the “Gettysburg Address” would propose a team of monkeys as author.
A similar example of repeated independent trials used as a mechanism for obtaining order from disorder is chemical evolution. Because of its philosophical implications, however, the example is more controversial.
There are actually 172 symbols in the first sentence of the “Gettysburg Address” (adjusting the text to all lowercase with no punctuation and with “four score” being two words, as in the original), but applying the same math yields an upper bound on the probability at 10-219, a number that for most computing devices is indistinguishable from 0. To put that in perspective, if I were to mark a single atom (of the 1082 atoms that physicists estimate exist in the entire known observable Universe) and ask you to guess which one I marked, and you guessed correctly on the first try, the odds would have been better by a factor of 10137 than the odds of one in a billion monkeys accidentally typing the first sentence of the “Gettysburg Address.”
This is just one example, but you can find others in the mathematical literature, demonstrating how complex information does not occur by accident in finite scenarios–which are the only scenarios that actually exist. Maybe Roberts didn’t feel that this example was controversial or didn’t present philosophical implications, but I would argue that it certainly does pose moral implications given that DNA is arguably the most complex informational structure known to humanity. I will post an excerpt of the “controversial” example shortly.
