Monkey math | By the Hearing of Faith

In a previous post, I wrote that complexity and specification never spontaneously arise unassisted from the chaos of a random non-intelligent source. You’d think that would be a reasonable statement that anyone could agree with, but from time to time I encounter people who seem to believe not only that chance is a causal agent rather than merely an attribute of a given scenario (e.g., “The Universe happened by chance”) but also that chance combined with time results in anything we can assume from the standpoint of naturalist philosophy. Consequently, what seems reasonable ends up being dismissed as superstition, and the justification given is often some variation of the Infinite Monkey Theorem, which usually goes unchallenged in casual conversation because most people (myself included) aren’t fluent enough in probability theory to object.

About five years ago, I was browsing through an introduction to applied probability and found the following example in a chapter on repeated independent trials (Roberts, Richard A. “Independence and Repeated Trials.” An Introduction to Applied Probability, Addison-Wesley, 1992, pp. 88–89). While still not succinct enough for a casual conversation, it’s probably concise enough for someone with good math-ninja skills (like John Lennox) to present in a formal debate. It’s very compelling.

Example 3.5.2

Suppose a billion monkeys type on word processors at a rate of 10 symbols per second. Assume that the word processors produce 27 symbols, namely, 26 letters of the English alphabet and a space. These monkeys type for 10 billion years. What is the probability that they can type the first sentence of Lincoln’s “Gettysburg Address”?

Fourscore and seven years ago our fathers brought forth on this continent a new nation conceived in liberty and dedicated to the proposition that all men are created equal.

Solution: If we counted correctly, there are 168 symbols in this sentence. Let N be the number of symbols typed per monkey in 10^10 years. A sample space of possible letter sequences typed by each monkey is

S = X * X * ... * X (N times)

where X is the set of 27 symbols. Now define s as a particular sequence that is m symbols long:

s = s_1 s_2 ... s_m.

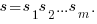
Let 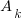be the event that s appears at the index in a sequence of length N:

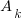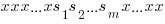= { ( occurs on index k)}

In other words, 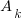is the event that a particular sequence, s, which is m symbols long, appears in one monkey’s sequence and ends on index k. The event of interest is A, given by

$A=bigcup{k=m}{N}{A_{k}}.$

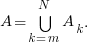
In our case, m = 168 and N is the number of symbols typed by one monkey in 10^10 years. Thus by Boole’s Inequality,

$P delim{[}{A}{]} = P {[}{bigcup{k=m}{N}{A_{k}}}{]} <= {sum{k=m}{N}{P delim{[}{A_k}{]}} }.$

Now the probability of the event 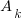is the number of outcomes of event 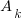divided by the total number of outcomes. The total number of outcomes is 27^N . The number of outcomes that produce event 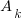is $27^{N-m}$ . The exponent is 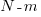because there are m positions specified in 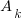. The remaining 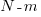are arbitrary. Thus

$P delim{[}{A_k}{]} = {27^{N-m}}/{27^N} = 1/{27^m}.$

And so

$P delim{[}{A}{]} <= {sum{k=m}{N}{(1/{27^m})}} = {N - m + 1}/{27^m} approx N/{27^m}$

since N >> m. Thus is bounded above by $N/{27^m}$ , where N is the number of trials produced by a single monkey. This is the probability bound for for one monkey. For 10^9 monkeys, we can think of forming one long sequence by concatenating 10^9 sequences so that N becomes the number of trials produced by 10^9 monkeys. Thus is bounded above by

$<= {10^9}*(10^7 seconds-per-year)(10 symbols-per-second)(10^10 years) approx {10^27}/{10^240} <= 10^{-213}.$

The probability of producing a specified sequence of English text 168 symbols long is bounded above by 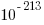$10^{-213}$ . No reasonable model for the source of the “Gettysburg Address” would propose a team of monkeys as author.

Actually, there are 171 characters (minus the period), and the string should be written all in upper or lower case, but the point of the exercise is still valid. Roberts calculates the probability of the string occurring anywhere (from index position 168 to the last typed character) over the total number of characters a single hypothetical monkey could type in 10 billion years (N characters). He then uses Boole’s Inequality to establish an upper bound for that probability (i.e., the probability is no higher than the right side of that inequality) and then scales the scenario up by 10^9 (1 billion monkeys). The denominator in the last approximation is a power of ten to make it more readable, and 27^168 (2.95e+240) is for all intents and purposes close enough to 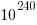10^240 (1.0e+240). (Anyone who’s seriously thought about the origin of information has likely already taken note that scenarios like the Infinite Monkey Theorem assume an infinite event space encompassing all probabilities/possibilities.)

Roberts then adds, “A similar example of repeated independent trials used as a mechanism for obtaining order from disorder is chemical evolution. Because of its philosophical implications, however, the example is more controversial.”

Controversial! Well, I guess I’ll have to reproduce that example, too ….